date_range 07/08/2020 23:39

1. Cross entropy

• Cross-entropy is a measure the difference between two probability of distributions $p$ and $q$, denoted as:
  $$\mathbf{H}(p,q)=-\int p(x)\log q(x)\text{d}x$$
• Cross-entropy calculates the number of bits required to represent or transmit an average event from one distribution compared to another distribution. In formula $(1)$, $p(x)$ is the target distribution, $q(x)$ is the approximation of the target distribution.
• By Lagrange multiplier method, we can prove $\mathbf{H}(p,q)$ reaches the minimum value when $p(x)=q(x)$, it means:
  $$\begin{align} \min \mathbf{H}(p,q)&=\mathbf{H}(p,p)\\ &=-\int p(x)\log p(x)\text{d}x=\H[p]\tag2 \end{align}$$

date_range 19/06/2020 16:39

• In this blog, we will discuss about Information theory, about its concept and its mathematical nature.

date_range 14/06/2020 09:52

2.3. The Gaussian Distribution

• The Gaussian, also known as the normal distribution, is a widely used model for the distribution of continuous variables. For single variable $x$, the Gaussian distribution can be written in the form:
  $$\mathcal{N}(x|\mu,\sigma^2)=\frac{1}{(2\pi\sigma^2)^{1/2}}\exp{\{-\frac{1}{2\sigma^2}(x-\mu)^2\}}\tag1$$
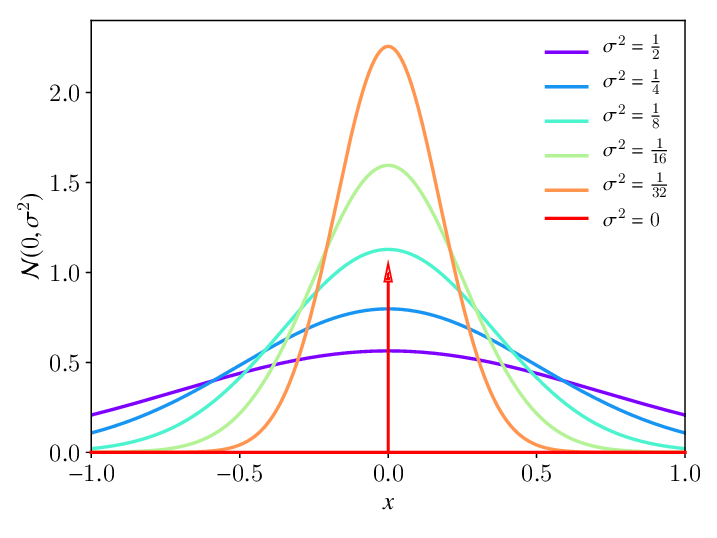
  where $\mu,\sigma^2$ are the mean and the variance respectively. Figure 1: 1-dimensional Gaussian distribution Source: https://www.researchgate.net/figure/Gaussian-bell-function-normal-distribution-N-0-s-2-with-varying-variance-s-2-For_fig1_334535945  
• For $D-$dimensional vector $\mathbf{x}$, the multivariate Gaussian distribution takes the form:
  $$\mathcal{N}(\mathbf{x}|\vec\mu,\Sigma)=\frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp{\{-\frac{1}{2}(\mathbf{x}-\vec\mu)^\top\Sigma^{-1}(\mathbf{x}-\vec\mu)\}}\tag2$$
  where the mean and the covariance matrix was mentioned in ML&PR_2.

date_range 29/05/2020 08:30

• We have introduced the matrix decomposition in DL_1 which have many applications. In this article, we will discuss about using the matrix decomposition to obtain the best possible approximation of a given matrix, called a matrix of low rank.
• A low rank approximation can be considered a compression of the data represented by the given matrix.

date_range 14/05/2020 10:22

• You should read about eigenvectors and eigenvalues in MATH_6 to be able to understand the following.