2.2. Tối thiểu rủi ro thực nghiệm

• Như đã đề cập ở phần trước, một thuật toán học có đầu vào là tập huấn luyện $S$ được lấy mẫu bởi phân bố $D$ không biết trước và được gán nhãn bằng hàm $f$. Đầu ra của thuật toán học là hàm dự đoán $h_S:X\to Y$. Mục đích của thuật toán là tìm hàm $h_S$ với sai số trên $D$ là nhỏ nhất.

• Tuy nhiên, $D$ và $f$ không biết trước nên ta không thể tìm được lỗi thật (true error, lỗi trên $D$) của bộ học mà chỉ có thể tính được lỗi trên tập huấn luyện (lỗi trên $S$):

với $[m]=\{1,...,m\}]$.

• Ở góc nhìn khác, hàm lỗi thể hiện xác suất đoán đúng của hàm dự đoán. Lỗi này được gọi là sai số thực nghiệm (empirical error). Vì vậy, nếu bộ dữ liệu huấn luyện $S$ đại diện cho dữ liệu "thật" (dữ liệu trên $D$), ta có thể tối thiểu $L_s(h)$ với hi vọng $L_D(h)$ cũng được tối thiểu - được gọi là "Tối thiểu rủi ro thực nghiệm" (Empirical Risk Minimization) hay ERM.

2.2.1. Overfitting

• Phương pháp ERM có thể dẫn đến một kết quả tồi. Trước tiên hãy xem xét ví dụ sau:

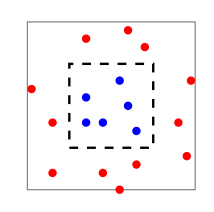
• Một bộ học muốn dự đoán trái đu đủ đã chín hay chưa dựa vào độ mềm và màu sắc. Giả sử với $D$ là phân phối đều và hàm gán nhãn $f$ là hình vuông nét đứt, với các điểm bên trong được gán nhãn $1$ và $0$ với các điểm bên ngoài. Diện tích hình vuông lớn là $2$, hình vuông nhỏ là $1$. Xem xét hàm dự đoán sau:

• Hàm dự đoán trên có vẻ "thông minh" khi với rủi ro thực nghiệm $L_S(h)=0$. Tuy nhiên, mục đích cuối cùng của việc học vẫn là tối thiểu $L_D(h)$ chứ không phải $L_S(h)$. Trong trường hợp này, hàm dự đoán cho kết quả đúng với các điểm đã biết ($h_S(x)=y_i$ với $x=x_i$) và các điểm có nhãn $0$ (các điểm ngoài hình vuông nhỏ; $h_S=0$ với những điểm không thuộc tập dữ liệu). Do đó, $L_D(h)=1/2$.

• Hàm dự đoán trên là một ví dụ về overfitting, khi mà bộ học học tốt trên dữ liệu huấn luyện nhưng có hiệu suất kém trên dữ liệu thực.