1. Phân phối đều (Uniform):

• $x\in S_x=[a,b]$

• $f(x)=\frac{1}{b-a}$, $a\le x\le b$

  

• $E[x]=\frac{a+b}{2}$, $VAR[x]=\frac{(b-a)^2}{12}$

2. Phân phối mũ (Exponential):

• $x\in S_x=[0,\infty)$

• $f(x)=\lambda e^{-\lambda x}$, $\lambda>0$, $x\ge0$

  

• $E[x]=\frac{1}{\lambda}$, $VAR[x]=\frac{1}{\lambda^2}$

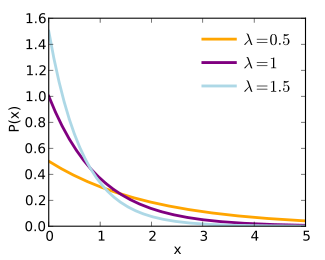
• Note:

  • $\lambda$ là số biến cố trung bình xảy ra trong một đơn vị thời gian.

  • $x$ là số đơn vị thời gian cho đến khi biến cố kế tiếp.

  • Phân phối mũ mô tả xác suất thời gian giữa các lần sự kiện xảy ra trong phân phối Poisson.

  • Phân phối mũ có tính không nhớ (memoryless property) , nghĩa là:

    • $P[X>t+h|X>t]=P[X>h]$

    • Chứng minh:

      $$\begin{align} P[X>t+h|X>t] &=\frac{P[\{X>t+h \}\cap\{X>t \}]}{P[X>t]} \\ &=\frac{P[X>t+h]}{P[X>t]} \\ &=\frac{e^{-\lambda(t+h)}}{e^{-\lambda t}} \\ &=e^{-\lambda h} &=P[X>h] \end{align}$$

3. Phân phối Gauss (Normal):

• $x\in S_x=(-\infty,\infty)$

• $f(x)=\frac{e^{-(x-m)^2/2\sigma^2}}{\sqrt{2\pi}\sigma}$ với $\sigma>0$

  

• $E[x]=m$, $VAR[x]=\sigma^2$

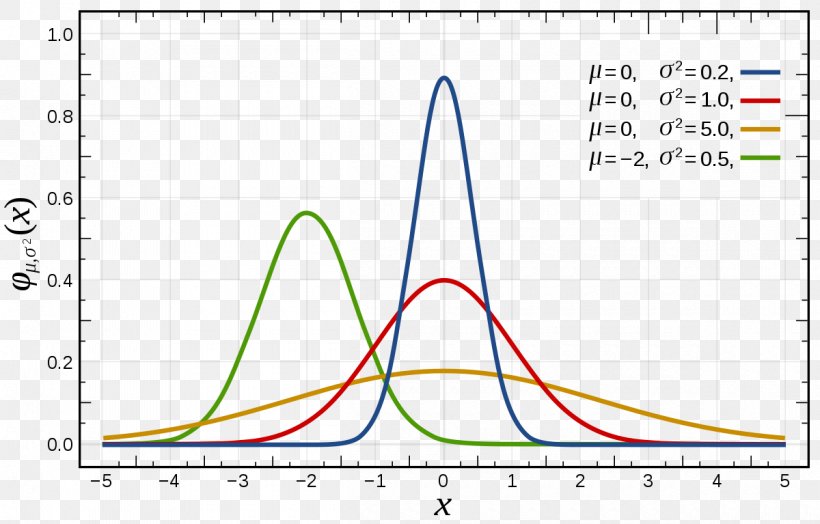
• Note:

  • Phân phối Gauss xuất hiện thường xuyên trong các vấn đề liên quan đến sự ngẫu nhiên.

  • Hàm tích lũy xác suất:

    $$\begin{align} P[X\leq x]&=F(x) \\ &=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{(x-m)/\sigma}(e^{-t^2/2})dt \\ &=\Phi(\frac{x-m}{\sigma}) \end{align}$$

  • Q-function:

    $$Q(x)=1-\Phi(x)$$

    • Công thức xấp xỉ:

      $$Q(x)\approx[\frac{1}{(1-a)x+a\sqrt{x^2+b}}]\frac{1}{\sqrt{2\pi}}e^{-x^2/2}$$
      • với: $a=\frac{1}{\pi}, b=2\pi$

4. Phân phối Gamma:

• $x\in S_x=(0,\infty)$

• $f(x)=\frac{\lambda (\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

  • với:

    • $\alpha>0, \lambda>0$

    • $\Gamma(z)= \displaystyle \int_0^\infty x^{z-1}e^{-x}dx$

    • Một số tính chất của $\Gamma()$:

      • $\Gamma(\frac{1}{2})=\sqrt{\pi}$
      • $\Gamma(z+1)=z\Gamma(z)$ với $z>0$
      • $\Gamma(m+1)=m!$ với $m$ nguyên dương

  • Minh họa: Với $k=\alpha$, $\theta=\frac{1}{\lambda}$

    

• $E[x]=\alpha /\lambda$, $VAR[x]=\alpha/ \lambda^2$

4.1. m-1 Erlang:

• Với $\alpha=m$, $m$ là số nguyên dương:

  • $f(x)=\frac{\lambda e^{-\lambda x}(\lambda x)^{m-2}}{(m-1)!}$

• Phân phối m-1 Erlang mô tả thời gian cho đến khi $m$ biến cố ngẫu nhiên liên tiếp xảy ra.

4.2. Chi-Square:

• Với $\alpha=k/2$ ($k$ nguyên dương) và $\lambda=1/2$:

  • $f(x)=\frac{x^{(k-2)/2}e^{-x/2}}{2^{k/2}\Gamma(k/2)}$

• Phân phối Chi-Square mô tả tổng bình phương của $k$ zero-mean, unit-variance phân phối Gauss độc lập.

  • zero-mean: Kì vọng $E[x]=0$
  • unit-variance: Độ lệch chuẩn $\sqrt{VAR[x]}=1$

• Chi-Square được sử dụng rộng rãi trong thống kê để:

  • Ước lượng khoảng tin cậy cho độ lệch chuẩn của tập tổng thể đối với một phân phối chuẩn, sử dụng độ lệch chuẩn của mẫu.
  • Để kiểm tra độ độc lập của hai phân loại tiêu chuẩn đối với các biến đa tính.
  • Để kiểm tra mối quan hệ giữa các biến phạm trù.
  • Để nghiên cứu độ biến thiên mẫu trong trường hợp phân phối là phân phối chuẩn.
  • Để kiểm thử độ lệch giữa các tần số kỳ vọng và tần số thực tế.
  • Để thực hiện kiểm thử Chi-Square (một kiểm thử rất hiệu quả cho sự tương thích).

5. Phân phối Beta chuẩn:

• $x\in S_x=(0,1)$

• $f(x)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\Beta(\alpha,\beta)}$, với:

  • $\alpha>0$, $\beta>0$
  • $\Beta(\alpha,\beta)=\displaystyle\int_0^1x^{\alpha-1}(1-x)^{\beta-1}dx=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$

  

   

• $E[x]=\frac{\alpha}{\alpha+\beta}$, $VAR[x]=\frac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)}$

• Note:

  • Với $\alpha=\beta=1$, ta có phân phối Uniform.
  • Với $\alpha-1=p$ và $\beta-1=1-p$ ($0\le p\le 1)$, ta được phân phối Bernoulli.
  • Phân phối Beta hữu ích do đồ thị phân phối xác suất rất linh hoạt

6. Phân phối Laplacian:

• $x\in S_x=(-\infty,\infty)$

• $f(x)=\frac{1}{2b}e^{-\frac{\vert x-\mu\vert}{b}}$ với $b>0$

  

• $E[x]=\mu$, $VAR[x]=2b^2$

7. Phân phối Rayleigh:

• $x\in S_x=[0,\infty)$

• $f(x)=\frac{x}{\sigma^2}e^{-x^2/2\sigma^2}$ với $\sigma>0$

  

• $E[x]=\sigma\sqrt{\pi/2}$, $VAR[x]=(2-\pi/2)\sigma^2$

• Ứng dụng:

  • Truyền thông – để mô hình hóa các đường đi của tín hiện bị phân tán dày đặc tới bộ tiếp nhận.
  • Khoa học vật lý – để mô hình hóa tốc độ gió, chiều cao sóng, âm thanh hoặc bức xạ ánh sáng.
  • Kỹ thuật – để kiểm tra tuổi thọ của một vật thể dựa trên tuổi hiện tại của nó.
  • Ảnh hóa y tế - để mô hình hóa biến đổi nhiễu trong ảnh chụp cộng hưởng từ.

8. Phân phối Cauchy:

• $x\in S_x=(-\infty,\infty)$

• $f(x)=\frac{\lambda/\pi}{(x-x_0)^2+\lambda^2}$ với $\lambda>0$, $-\infty\le x_0\le \infty$

  

• Note:

  • Phân phối Cauchy là một trong những phân phối xác suất đặc biệt vì kỳ vọng và phương sai không tồn tại.
  • Trong vật lý, phân phối này có liên quan đến nhiều quá trình, trong đó có phân phối năng lượng cộng hưởng.

Tham khảo:

[1] Phân phối xác suất

[2] Chi-Square

[3] Phân phối mũ

[4] Laplacian Distribution

[5] Phân phối Beta

[6] Phân phối Rayleigh

[7] Phân phối Cauchy | Phân phối xác suất | Wiki

[8] Book: Probability, Statistics, and Random Processes for Electrical Engineering (Alberto Leon-Garcia)