Convolution (tích chập) là kỹ thuật quan trọng trong xử lý tín hiệu số nói chung và xử lý ảnh (Image processing) nói riêng. Convolution được sử dụng chính yếu trong các phép toán trên ảnh như: đạo hàm ảnh (gradient image), làm trơn ảnh (blurring), nhận diện viền (edge detection), trích xuất đặc trưng (feature extraction).

Bài viết này cung cấp cho bạn kiến thức cơ bản về Convolution và tính chất của nó.

1. Giới thiệu về toán tử tuyến tính

• Một toán tử (hệ thống) $H$ được gọi là tuyến tính (linear) nếu thỏa mãn cả hai tính chất sau:

  • Tính chất cộng:

    $$H(u_1+u_2)=H(u_1)+H(u_2) \tag3$$

  • Tính chất nhân:

  $$H(\alpha u_1) = \alpha H(u_1) \tag3$$

   

  • Trong đó:

    • $u_1$, $u_2$ là các tham số
    • $\alpha$ là một số thực

• Trong Tín hiệu và hệ thống, $u_1$ & $u_2$ được gọi là tín hiệu vào, $H$ được gọi là hàm biến đổi.

• Ví dụ :

  • $H(x)=2x$ tuyến tính vì chúng ta dễ thấy:

    • $H(x1+x2)=2(x1+x2)=2x1+2x2=H(x1)+H(x2)$

       

    • $H(3x)=2.3x=3.2x=3H(x)$

    • Một trường hợp dễ gây hiểu lầm, đó là $H(x)=x+1$. Nhìn có vẻ tuyến tính nhưng thật ra không phải vậy. Ta sẽ xem xét nó dựa trên hai tính chất ở trên:

      $$\begin{align} H(x1+x2)&=x1+x2+1 \\\ &=(x1+1)+(x2+1)-1 \\\ &=H(x1)+H(x2)-1\\\ &\not=H(x1)+H(x2) \end{align}$$

• Trong bài (Nhập môn Filtering) có nhắc đến khái niệm bộ lọc tuyến tính, qua các tính chất ở trên, ta có thể định nghĩa: "Một bộ lọc tuyến tính là một bộ lọc mà giá trị các output pixel có quan hệ tuyến tính với các pixel lân cận của nó."

2. Cross-correlation và convolution

2.1. Cross-correlation (tương quan chéo)

• Bạn đọc nên tìm hiểu trước về Correlation Filter ở bài (Nhập môn Filtering)

• Cross-correlation:

  • Công thức với kenel có kích thước $(2k+1)\times(2k+1)$:

    $$G[i,j] = \sum\_{u=-k}^{k}\sum\_{v=-k}^{k}H[u,v]F[i+u,j+v] \tag4$$

  • Ký hiệu:

  $$G = H \otimes F$$
  • Cross-correlation giúp tìm kiếm sự tương quan của kernel trên ảnh gốc. Bạn có thể thấy vùng pixel trên ảnh gốc càng tương quan với kernel thì giá trị output càng lớn.

2.2. Convolution (Tích chập)

• Convolution là toán tử mà ta xoay thực hiện xoay kernel 180 độ (flip over, tức flip 2 lần lần lượt theo trục x và y) rồi áp dụng phép correlation.

  

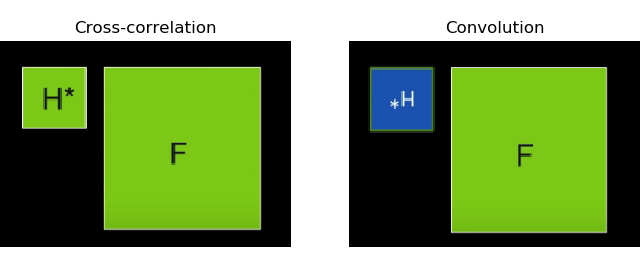
  Nguồn: Introduction in Computer Vision (Udacity)

   

  • Công thức:

    $$G[i,j] = \sum\_{u=-k}^{k}\sum\_{v=-k}^{k}H[u,v]F[i-u,j-v] \tag5$$

  • Ký hiệu:

    $$G = H \ast F$$

  • Giá trị tâm kernel được gọi là điểm neo (anchor point).

2.3. Convolution có gì hơn cross-correlation?

• Cả Convolution và cross-correlation đều là bộ lọc tuyến tính.

• Sự khác biệt duy nhất mà chúng ta thấy được qua công thức trên là: convolution lật ngược kernel rồi mới thực hiện sliding window. Tuy nhiên chính điều này đã tạo nên tính chất riêng của convolution mà cross-correlation không có:

  • Tính giao hoán:

    $$f\ast g = g\ast h \tag7$$

  • Tính phân phối:

    $$f\ast (g+h)=f\ast g +f\ast h \tag7$$

  • Tính kết hợp: Điều này thể hiện rằng thay vì ta lấy ảnh gốc $I$ convolve với kernel $K1$, sau đó lấy ảnh kết quả convolve với $K2$ thì ta có thể thực hiện lấy kernel $K1$ convole với $K2$ thành 1 kernel nào đó, sau đó lấy kernel kết quả này áp dụng cho ảnh gốc $I$. Chính nhờ tính chất này mà khi thiết kế kernel, thay vì thiết kế nhiều phép convolve tuần tự ta có thể kết hợp chúng lại thành 1 kernel duy nhất.

    $$f\ast g\ast h = f\ast (g\ast h) \tag7$$

  • Do đó trong Xử lý ảnh, convolution được sử dụng (thay vì correlation) để có thể xây dựng được một bộ lọc duy nhất bằng cách kết hợp nhiều bộ lọc lại với nhau. Sau đó có thễ dùng bộ lọc này để áp lên cơ sở dữ liệu ảnh lớn.

  • Ngoài ra, chính tính kết hợp này giúp ta có thể tối ưu hóa độ phức tạp của phép convolution trong lập trình. Điều này sẽ được làm sáng tỏ ở ngay dưới đây.

• Minh họa tính kết hợp:

  • Trong ví dụ này mình sử dụng hai ma trận: $Matrix1 = \frac{1}{9} \begin{bmatrix}1&1&1\\\ 1&1&1\\\ 1&1&1\end{bmatrix}$ và $Matrix2 = \frac{1}{16}\begin{bmatrix}-1&-2&-1\\\ -2&12&-2\\\ -1&-2&-1\end{bmatrix}$.

  • Ảnh gốc $I$:

    

  • $I \ast Matrix1$:

    

  • $I \ast Matrix2$:

    

  • $(I \ast Matrix1)\ast Matrix2$:

    

  • $(I \ast Matrix2)\ast Matrix1$:

    

  • $I \ast (Matrix1\ast Matrix2)$:

    

  • Code tham khảo xem ở đây.

2.4. Tối ưu hóa phép convolution

• Giả sử bạn có một bức ảnh $I$ có kích thước $N \times N$ pixels, một kernel $W\times W$. Khi thực hiện sliding window, ở mỗi vị trí, chúng ta phải thực hiện $W\times W$ phép nhân rồi cộng chúng lại với nhau. Để thực hiện trên toàn bộ $I$, chúng ta phải tính $N\times N\times W\times W = N^2W^2$ phép nhân, một con số rất lớn. Câu hỏi đặt ra bây giờ là: Làm thế nào để tối thiểu số lượng phép tính khi thực hiện convolution? Tính kết hợp của nó sẽ giúp ta trả lời câu hỏi này.

• Nếu bạn muốn thực hiện convolution với kernel $H = \begin{bmatrix}2&1&3\\\ 4&2&6\\\ 2&1&3\end{bmatrix}$, thay vì dùng nguyên ma trận này, bạn có thể tách ra như sau:

  $$H = \begin{bmatrix}2&1&3\\\ 4&2&6\\\ 2&1&3\end{bmatrix} = c\ast r=\begin{bmatrix}1\\\ 2\\\ 1\end{bmatrix}\ast\begin{bmatrix}2&1&3\end{bmatrix}$$

• Do đó ta có:

  $$G = H\ast I = (c\ast r)\ast I = c\ast (r\ast I)$$

• Trong trường hợp tổng quát, với $H$ có kích thước $W\times W$ thì $c$ và $r$ lần lượt có kích thước $W\times 1$ và $1\times W$. Lúc này bạn có thể thực hiện hai lần phép convolution với kernel nhỏ hơn. Độ phức tạp bây giờ là $2WN^2<W^2N^2$ vì ta thường lấy $W\eqslantgtr 3$.

• Tuy nhiên, không phải ma trận nào cũng phân tích được như trên. Vì vậy khi tối ưu thời gian tính toán convolution, đặc biệt trong Convolution Neural Network, người ta không dùng cách trên. Bạn đọc có thể xem thêm ở đây.

2.5. Áp dụng trong Python

• Sau đây chúng ta sẽ thử áp dụng convolution và cross-correlation với kernel $H = \begin{bmatrix}-1&0&1\\\ -2&0&2\\\ -1&0&1\end{bmatrix}$ cho tấm hình:

  

• Bước 1: Khai báo thư viện, load ảnh và tạo ma trận bộ lọc. Ở đây mình dùng module cv2.filter2D cho phép cross-correlation và scipy.ndimage.convolve cho phép convolution.

  import cv2
  import numpy as np
  from scipy import ndimage
  
  # Load ảnh
  img = cv2.imread('đường dẫn ảnh',0)
  
  # Khởi tạo ma trận bộ lọc
  kernel = np.asanyarray([-1,0,1,-2,0,2,-1,0,1]).reshape((3,3))
  

• Bước 2: Thực hiện cross-correlation

  corr = cv2.filter2D(img,-1, mat)
  

• Bước 3: Thực hiện convovlution

  # Chuyển ma trận ảnh về kiểu dữ liệu float
  imgFloat = img.astype(float)
  # Thực hiện convolution
  conv = ndimage.convolve(imgFoat,kernel)
  # Với output pixel < 0, đưa về giá trị 0
  conv = np.where(conv<0, 0, conv)
  # Với output pixel > 255, đưa về giá trị 255
  conv = np.where(conv>255, 255, conv)
  # Đưa ma trận về kiểu dữ liệu ban đầu 
  conv = conv.astype(np.uint8)
  

• Kết quả:

  

• Full code các bạn có thể xem ở đây

3. Boundary Issues

• Ở trên chúng ta có bàn về sliding window, về việc các kernel trượt trên ma trận ảnh. Vậy bạn có tự hỏi: Nếu kernel trượt một phần ra ngoài ma trận ban đầu thì sao?

  

• Nếu không muốn xử lý trường hợp này, bạn có thể giới hạn phạm vi hoạt động của kernel.

  

   

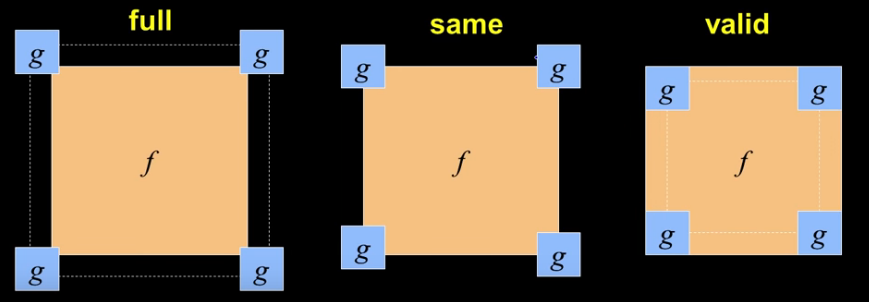
• Người ta chia làm 3 trường hợp như hình trên:

  • Valid: Đó là khi bạn không làm việc với các trường hợp kernel trượt ra ngoài ảnh. Như vậy ảnh output có size là: $size(output) = size(input)-size(kernel)+1$. Nhỏ hơn kích thước ảnh ban đầu.
  • Same: Ảnh output cùng kích thước với ảnh ban đầu: $size(output) = size(input)$
  • Full: Ảnh output có kích thước lớn hơn ảnh ban đầu: $size(output) = size(input)+size(kernel)-1$
  • Kết quả ở trên có được do mình mặc định $stride=[1,1]$, bạn đọc muốn tìm hiểu kĩ hơn có thể xem ở đây.

• Đôi khi bạn muốn đầu ra là ảnh có cùng kích thước hoặc có thể lớn hơn kích thước ảnh ban đầu, bạn phải sử dụng Same hoặc Full. Vì vậy bạn cần tạo các giá trị bên ngoài ma trận ảnh để kernel có thể tính toán khi trượt ra ngoài.

• Note: Tính phân phối của phép convolution chỉ đúng trong trường hợp boundary issues là Full.

• Kỹ thuật trên gọi là đệm (pad ). Dưới đây là các kỹ thuật padding phổ biến:

3.1. Constant padding (đệm hằng số):

• Giá trị identify của vùng đệm mang một giá trị $a$ duy nhất. Giá trị này phụ thuộc vào loại ảnh mà bạn muốn xử lý.

  

  Zero padding

   

• Nếu $a=0$, ta có zero padding. Điểm mạnh của zero padding là nó không tạo thêm đặc trưng (feature) cho ảnh. Đó là lý do zero padding được dùng nhiều trong các mô hình Deep Learning.

• Ví dụ 1:

  

  Zero padding

• Ví dụ 2:

  • Ảnh gốc:

    

  • Padding:

    

  • Làm mờ ảnh bằng Convolution:

    

    • Viền đen bao quanh ảnh là ảnh hưởng từ vùng đệm của zero padding.

     

3.2. Reflect padding (Đệm phản chiếu)

• Trong phương thức này, vùng đệm được lấy đối xứng từ vùng rìa ảnh qua các cạnh.

  

  Reflect padding

• Khi trích xuất đặc trưng (extract feature) bằng convolution, phần cạnh sẽ bị bỏ qua. Reflect padding giúp bạn tạo ra thông tin "fake" bù vào phần đó. Tuy nhiên điều này không đúng trong mọi hoàn cảnh. Trong một số trường hợp reflect padding phá vỡ đặc trưng vốn có của ảnh.

• Reflect padding thường được dùng khi bạn quan tâm tới biểu đồ sáng (brightness histogram) và độ tương phản (contrast) của ảnh.

• Ví dụ 1:

  

  Reflect padding

  • Nếu bạn cần nhìn rõ hơn:

    

     

• Ví dụ 2:

  • Ảnh gốc:

    

  • Padding:

    

  • Làm mờ ảnh bằng Convolution:

    

   

3.3. Nearest neighbor padding

• Nearest neighbor padding sử dụng các pixel ngoài cùng cho vùng đệm.

  

  Nearest neighbor padding

• Ví dụ:

  

  Nearest neighbor padding

• Ví dụ 2:

  • Ảnh gốc:

    

  • Padding:

    

  • Làm mờ ảnh bằng Convolution:

    

3.4. Wrap padding

• Khó mà giải thích bằng lời về wrap padding, bạn có thể hiểu qua các ví dụ sau:

  

  Wrap padding

• Ví dụ 2:

  • Ảnh gốc:

    

  • Padding:

    

  • Làm mờ ảnh bằng Convolution:

    

    • Viền trên có màu đỏ do ảnh hưởng từ vùng đệm lầy từ viền dưới ảnh. Qua đó khi làm mờ khiến ảnh có gì đó không đúng so với ảnh gốc.

Ở trên là 4 ví dụ Convolution ảnh sau khi padding (cụ thể hơn là làm mờ ảnh), ta có thể thấy Reflect và Nearest neighbor có kết quả tốt hơn 2 phương pháp còn lại. Ví dụ trên giúp bạn hình dung trực quan hơn về các phương pháp padding và có thể lựa chọn các phương pháp phù hợp cho bài toán của riêng mình.

Thư viện OpenCV hỗ trợ khá đầy đủ phần này, các bạn có thể tham khảo ở đây.

Tổng hợp các phương pháp padding ở trên:

Tham khảo:

[1] Introduction to Computer Vision | Udacity

[2] Introduction to Computer Vision | Cornell

[3] Linearity | Wiki

[4] Cross-correlation | Wiki

[5] Convolution | Wiki

[6] Convolution | minhng.info

[7] Tích chập | STDIO

[8] Cross-correlation vs Convolution

[9] Making border in OpenCV

[10] Why use symmetric padding?

[11] Why use reflect padding?

[12] Biến đổi tuyến tính | Wiki